TITLE: Diagrams to summarise Biodiversity - Ecosystem Function Research DATE: 2021-06-01 AUTHOR: John L. Godlee ==================================================================== I've been writing the background and introduction chapter of my PhD thesis. In it, I write about previous research into the "Biodiversity - Ecosystem Function Relationship", the idea that variation in biodiversity affects the way ecosystems function. To visualise some of the breakthroughs over the last 30 or so years I decided to make a schematic diagram. The diagram is below, with the lengthy caption I included in the chapter. 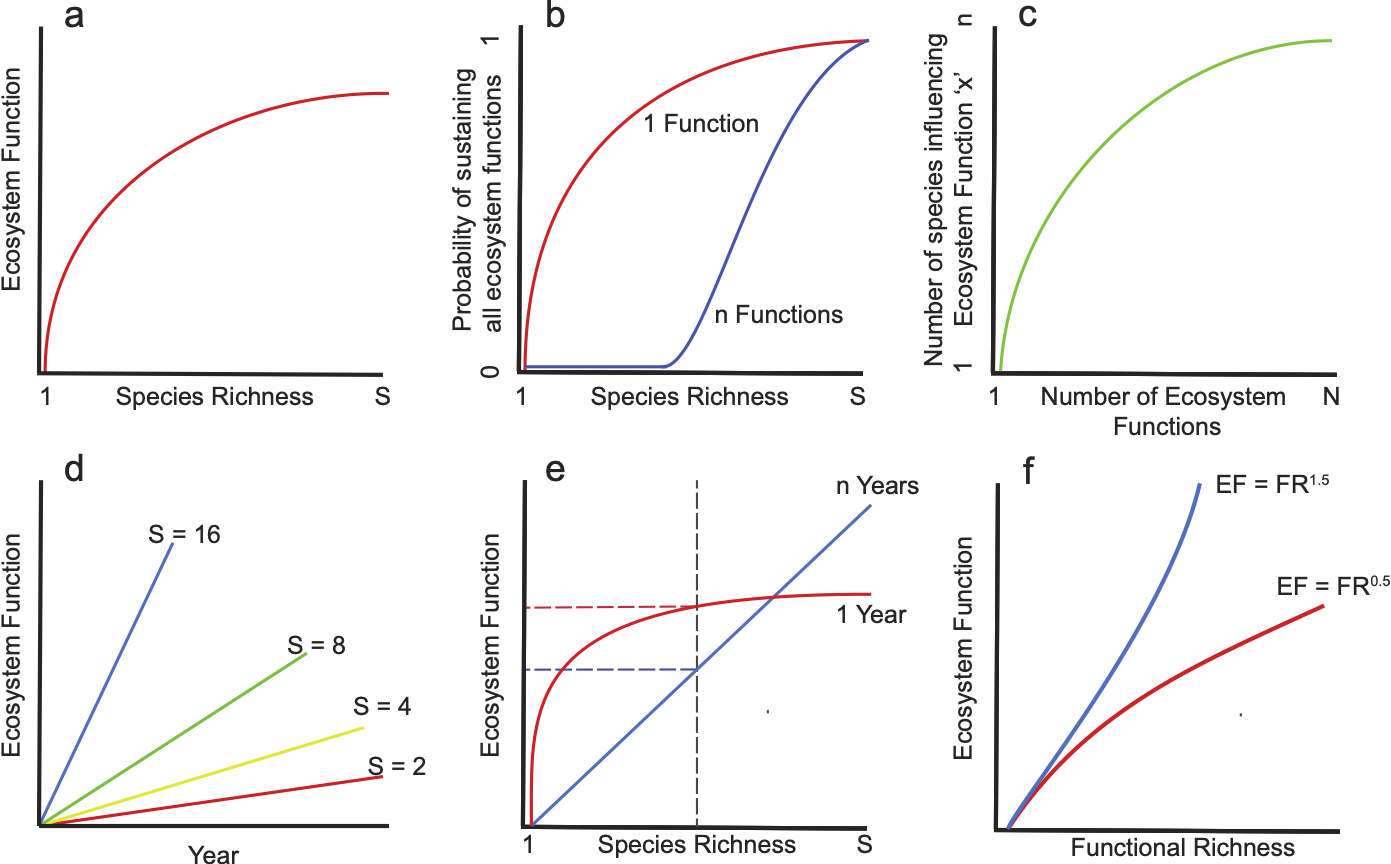 Schematic diagrams illustrating various inferences made on the Biodiversity - Ecosystem Function Relationship by previous studies. a) The classic BEF relationship found by many small scale experiments (Cardinale, Srivastava, et al., 2009). b) As more functions are considered simultaneously the minimum species richness needed to maintain overall ecosystem functionality increases, also showing how the proportion of functionally redundant species increases as less functions are considered (i.e. the curve reaches asymptote at a lower species richness) (Hector and Bagchi, 2007). c) The saturating relationship of the number of ecosystem functions considered and the number of species influencing ecosystem multifunctionality (Hector and Bagchi, 2007). d) As studies progress through time the strength of the BEF relationhip increases, the rate of increase in ecosystem function increases as species richness (S) grows (Cardinale, J. P. Wright, et al., 2007). e) As studies progress through time the shape of the relationship becomes more linear, saturating at progressively higher species richnesses. Studies averaged over longer periods exhibit a greater loss in ecosystem function in response to an equivalent species richness reduction (Reich, D. Tilman, et al., 2012). f) When functional richness is used in place of species richness, the relationship reaches asymptote at a higher richness. Additionally the relationship becomes more concave as a power coefficient representing the strength and number of species interactions increases. FR gt1 (interspecific competition greater than intraspecific competition (unstable)) results in a convex relationship, while FR lt1 results in a concave relationship (Mora, Danovaro, and Loreau, 2014).