TITLE: A method to crop hemispherical images to a field of view
DATE: 2018-09-12
AUTHOR: John L. Godlee
====================================================================
For hemispherical photography of forest canopies, sometimes it's
necessary to crop the circular image to exclude a certain field of
view below the zenith angle. This might be because the lens
distorts the image too much below a given angle. Additionally,
because the calculation for LAI assumes random leaf orientation, an
assumption which is often broken, lower angles where leaf
orientation has a large effect on the relationship between gap
fraction and LAI can be excluded, typically below 60 degrees.
Cropping an image to a given field of view, where the image has
been projected onto a flat surface isn't that easy however.
Here is a function I wrote in R to calculate the number of pixels
of the radius of a circle equal to a given number of degrees field
of view, given the relationship between lens curvature and sensor
size.
fov_px <- function(theta, circle_diam_px, focal_length_mm,
theta_max){
library(NISTunits)
rads_theta <- NISTdegTOradian(theta - 1)
circle_radius_px <- circle_diam_px / 2
R <- ((2*focal_length_mm) * sin(rads_theta / 2))
max_rads_theta <- NISTdegTOradian(theta_max)
sensor_circle_radius_mm <- 2 * focal_length_mm *
sin(max_rads_theta / 2)
sensor_px_per_mm_flat <- circle_radius_px /
sensor_circle_radius_mm
pixels_per_theta <- R * sensor_px_per_mm_flat
print(pixels_per_theta)
}
The first thing the function does is convert the desired degrees
field of view to radians. Then it converts the pixel diameter of
the circular projected image into a radius. Then it uses an
equation for projecting equisolid images onto a flat plane, i.e.
the image sensor. This equation gives the number of mm from the
centre of the sensor an object will appear on the sensor and
therefore the flat image, given the focal length. The next step
calculates R for the maximum theta of the lens, in most cases 90
degrees for a full hemispheric image. This maximum R value can be
related to the pixel length of the full image to create a value of
pixel circle radius per theta degree value.
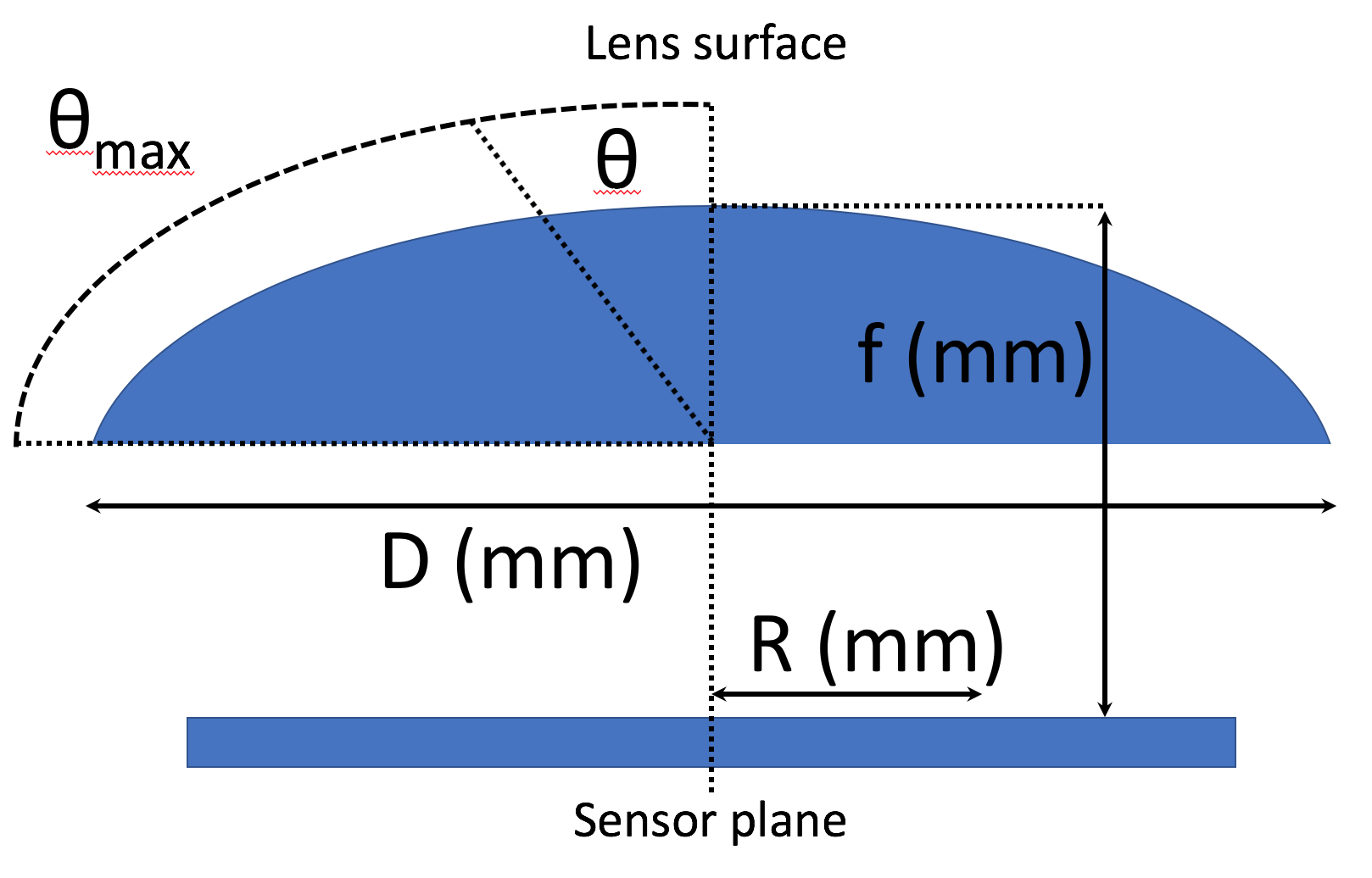
Here is a diagram which roughly describes the various values used
in the function, though the focal length is normally just taken
from the given focal length of the lens:
Then, it's easy enough to take the value given by fov_px and plug
it into this macro in ImageJ to crop the image to the desired pixel
radius:
circle_radius = <ADJUST_TO_fov_px()_OUTPUT>
makeOval(
(getWidth/2) - (0.5 * circle_radius),
(getHeight/2) - (0.5 * circle_radius),
circle_radius,
circle_radius))
run("Crop");
// Creates an elliptical selection, where (x,y) define the
upper left corner of the bounding rectangle of the ellipse.
// In this case, the ellipse is a circle and is centred on the
image